跳转至

Basic Segment Tree (To be modified)

定义

线段树和树状数组都是解决区间问题的数据结构，但与树状数组相比更易理解，但是实现代码比较长。

线段树融合了分治算法、二叉树结构和\(Lazy-Tag\)技术思想。

基本结构

线段树是一棵二叉树，树上的节点是“线段”，即区间，如下图是一棵线段树

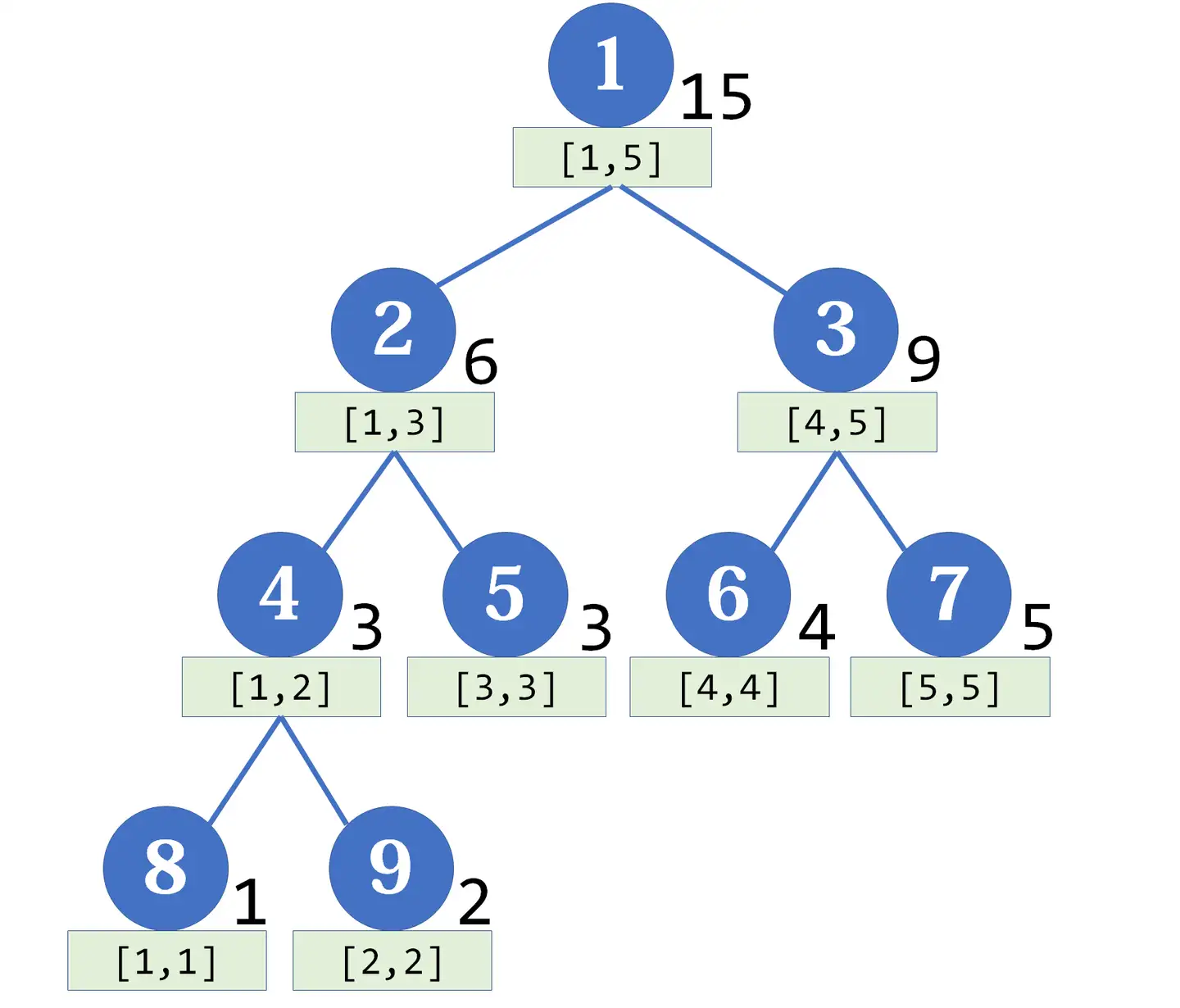
我们用分治法自定向下，每次分治，将区间分成左右两半，每一个节点维护一个这样的区间，节点所维护的线段所表示的值可以是区间和、区间最值等等，根据题目灵活定义。这样求解一个大区间的解可以有左右两个小区间合并而来。

线段树的构造

在竞赛中，一般用静态数组来实现满二叉树表示线段树，虽然比较浪费空间，但是易于编码。

定义静态数组实现满二叉树时，有两种实现方法，我们即可以定义结构体表示二叉树的节点，也可也直接用数组来实现。本文的实现都采用定义结构体的方式。

需要注意的是线段树空间要开到\(4N\)才能保证不越界访问。 

//定义结构体
struct{
    int l,r;//节点维护的区间
    int data;//节点维护的区间数据
}f[MAX << 2];
//定义数组
int f[MAX << 2];

在满二叉树中父节点与子节点之间的访问非常简单，父节点\(k\)的左右子节点为\(2\times k\)和\(2\times k+1\)

inline int ls(int k){return k<<1;}
inline int rs(int k){return k<<1|1;}

我们采用递归分治的方式构建线段树，每次将区间分为左右两部分，下面是现实：

inline void push_up(int k){
    f[k].data=f[ls(k)].data+f[rs(k)].data;//从下向上传递区间值
}
void build(int k,int l,int r){
    f[k].l=l,f[k].r=r;
    if(l==r){
        f[k].data=a[l];//叶子节点存原数组的值
        return;
    }
    int m=(l+r)>>1;//折半
    build(ls(k),l,m);//递归左儿子
    build(rs(k),m+1,r);//递归右儿子
    push_up(k);
}

线段树的基本功能

区间查询

线段树的区间查询非常简单，只要递归搜索线段树，将被搜索区间覆盖的区间节点累加到结果上即可。可以实现对区间最值，区间和的查询，下面以区间和为例，给出示例代码 

void ask(int k,int l,int r){
    if(l<=f[k].l&&r>=f[k].r)return f[k].data;
    int m=(f[k].l+f[k].r)>>1;
    int res=0;
    if(l<=m)res+=ask(ls(k),l,r);//与左节点有重叠
    if(r>m)res+=ask(rs(k),l,r);//与右节点右重叠
    return res;
}

时间复杂度为\(O(\log n)\)

区间修改

线段树的基本应用是单点修改。单点修改只要修改叶子节点的值，再从下至上的修改更新线段树即可，时间复杂度为\(O(\log n)\)。比较简单不详细介绍了。

P3372 【模板】线段树 1

题意：已知一个数列，你需要进行下面两种操作： 1 x y k :将[x,y]区间每一个数加上 k。 2 x y:输出区间[x,y]每一个数的和。

对于区间修改，我们就要用到\(Lazy-Tag\)技术。\(Lazy-Tag\)的核心思想就是通过延迟对节点信息的更改，从而减少可能不必要的操作次数。

在用\(Lazy-Tag\)方法时，若修改一个线段区间，就只对这个线段区间进行整体上的修改，其内部每个元素的内容先不做修改，只有当这个线段区间的一致性被破坏时（即查询或要修改其子区间时），才把变化值传递给下一层的子区间，我们称这个过程为下传标记，一般我们会单独写一个\(push\_down\)函数来完成这一操作。

我们可以额外定义一个\(tag\)数组或者在结构体中多加一个变量来记录每个线段区间的标记。

动态开点

动态开点顾名思义，就是在查询过程中动态的开辟线段树的节点，而不是一次将树完整的建出来，我们只初始化一个根节点，即整个区间。

因为我们是在需要某个节点时才开辟它，所以不能再使用堆式储存求左右儿子的公式，而是使用\(ls\)和\(rs\)数组记录对应节点的左右儿子，或者在结构体中加入两个变量来记录左右儿子的编号。

以区间和查询和单点修改为例为例 

//root代表整个树的根，cnt记录开辟的节点个数
int root,cnt,n;
int sum[n<<1],ls[n<<1],rs[n<<1];


//在x位置加上d
void update(int& k,int l,int r,int x,int d)
{
    //节点为空时，开辟一个新节点
    //类似于字典树和链式前向星的加边
    if(!k) k = ++cnt;
    if(s==t)
    {
        sum[k] += d;
        return;
    }
    int m = (l+r)>>1;
    if(x<=m)update(ls[k],l,m,x,d);
    else update(rs[k],m+1,r,x,d);
} 

//区间[s,t]查询
int ask(int& k,int l,int r,int s,int t);
{
    //一开始整个区间的和为0，即每个元素都为0
    //如果该区间还未开辟，说明区间和为0
    if(!k) return 0;

    //下面就是一般的线段树的区间和查询
    if(s<=l&&t>=r)return sum[k];
    int m = (l+r)>>1;
    int ans = 0;
    if(s<=m)ans+=ask(ls[k],l,m,s,t);
    else if(t>m)ans+=ask(rs[k],m+1,r,s,t);
    return ans;
}
我们会发现实际上就是在每个操作前加了一个开辟节点的代码。区间修改时也是类似，下沉标记时如果子节点还未开辟，就要先开辟子节点，在进行基础的线段树操作即可。

但这样有一个局限，我们维护的区间初始值必须全部一样，因为只创建了根节点，我们无法确定每个位置的值。例如维护区间和时，如果只开辟根节点，我们只知道整个区间的和，而不知道其子区间具体的和。所以一般动态开点线段树用与优化权值线段树（如主席树）的空间。

线段树的基础应用

特殊的区间修改

Can you answer these queries?

题意：对区间求每个数的开方，输出区间查询 元素个数\(N\le 10^5\)，元素之和不超过\(2^{63}\)，操作次数\(M\le 10^5\)

对于该题很容易我们能发现一个不超过\(2^{63}\)的数开方的次数不会超过\(7\)次，所以我们对于不等于\(1\)的数单独修改它，再递归的修改其父节点；当一个区间的数都为\(1\)时，就不对该区间进行修改。

复杂度：每个数开发\(7\)次，共\(7N\)次，在做\(M\)次修改复杂度为\(M\log N\)

同时做多种区间修改

P3373 【模板】线段树 2

如题，已知一个数列，你需要进行下面三种操作： - 1.将某区间每一个数乘上 x； - 2.将某区间每一个数加上 x； - 3.求出某区间每一个数的和。

我们设维护的区间和为\(sum\)，当我们可以将其看成\(1\times sum+0\)，当我对其进行一次操做\(2\)和操做\(1\)时，区间和变为\(k_1sum+b_1\)，我们再重复一边操做得到:

\[ k_2(k_1sum+b_1)+b_2=k_2k_1sum+k_2b_1+b_2 \]

我们要维护两种标记\(add 、multi\) 可见我们对区间标记修改时，先要做\(multi\)的修改，并且将\(add\)修改为\(add\times multi\)，再进行\(add\)修改。

进阶：Transformation

线段树的二分操做

Vases and Flowers 线段树的结构就是二分，在线段树上进二分答案非常方便，这题就是非常典型的二分答案，思路非常简单，用线段树进行区间更新的操做，在线段树上用二分法去找到放第一个花的位置，和最后一个花放的位置即可。

参考文章：
《算法竞赛-上册》-罗永军
CSDN_动态开点线段树
线段树-Oi Wiki